निर्धारक एक वर्ग मैट्रिक्स है लेकिन यह दो कोष्ठक के बजाय सीधी रेखा के नीचे है। हम इसका विस्तार कर सकते हैं और हम इसके मूल्य की गणना कर सकते हैं। सरल शब्दों में, एक निर्धारक एक वर्ग मैट्रिक्स से जुड़ी एक एकल संख्या है। संक्षेप में, हम निर्धारक को Det के रूप में लिखते हैं। A या | A | . याद रखें, गैर वर्ग आव्यूहों में निर्धारक नहीं होते हैं।
क्रम 2 के निर्धारक के मान की गणना करें
| a11 a12 |
| a21 a22 |
a11 X a22 - a12 X a21
for example
(4 5)
( 56 )
it is sequare matrix, its deteminant det. A =
| 4 5 |
| 5 6 |
4 X 6 - 5 X 5 = 24 - 25 = -1
Determinant of order 3
if matrix is square matrix of order 3 X 3, its determinant is possible
a 11 a 12 a 13
a 21 a 22 a 23
a31 a 32 a33
= a 11 | a 22 a 23 | - a 12 | a 21 a 23 | + a 13 | a 21 a 22 |
| a32 a 33 | | a31 a 33 | | a31 a 32 |
Now apply determinant formula of 2 order
= a11 ( a22 X a33 - a23 X a32) - a 12 ( a21 X a33 - a23 X a31) + a 13 ( a21 X a32 - a22 X a31)
निम्नलिखित उदाहरण में, आपने दो कोष्ठकों में मैट्रिक्स का मान दिया है और आपको निर्धारक के मान की गणना करनी है, बस पहली पंक्ति के प्रत्येक सह-कारक को पहली पंक्ति के तत्वों से गुणा करें और परिणामों का योग करें।
Other Languages


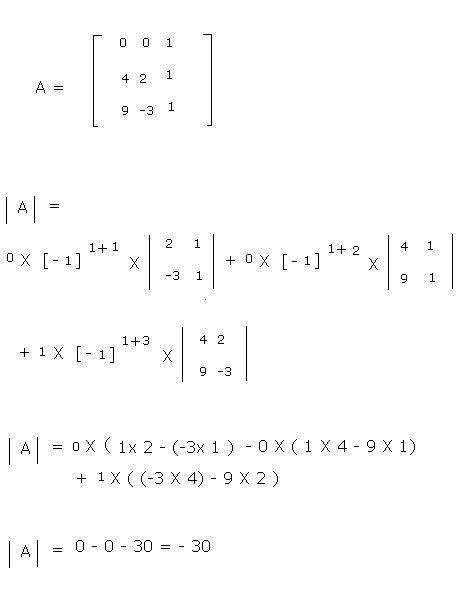
COMMENTS